【剑指offer-2】基础知识

编程语言

在面试过程中，面试官要么直接问语法，要么让用一种语言解决一个问题。在cpp中，一般考察编程语言的方式有以下三种：

  • 直接询问对cpp概念的理解：如cpp中的关键字，或者sizeof函数在各种情况下的值；
  • 分析写好的代码
  • 定义一个类型或实现类型中的成员函数

#1赋值运算符函数

题目：如下为类型CMyString的声明，请为该类型添加赋值运算符函数。

1
2
3
4
5
6
7
8
class CMyString {
    public:
        CMyString(char* pData=nullptr);
        CMyString(const CMyString& str);
        ~CMyString(void);
    private:
        char* m_pData;
};

在设计赋值运算符函数时需要考虑下面四个问题：

  • 返回值的类型声明与返回值：返回值的类型声明应该是该类型的引用，返回值应该是返回的实例自身的引用(*this)。考虑连续赋值的情况，如果函数返回值为空，不是返回的引用将不能连续赋值；
  • 传入的参数类型：传入的参数应该是常量引用，因为如果传入的参数不是引用而是实例的话，那么从形参到实参会调用一次复制构造函数，一般参数传递时使用引用来代替实例和指针，可以避免无谓的消耗，提高代码的效率，另外由于我们在函数中不用改变传入实例的状态，所以使用const；
  • 内存管理：是否释放实例自身已有的内存；
  • 特殊输入判断：判断传入的参数和当前的实例(*this)是不是同一个实例；
1
2
3
4
5
6
7
8
9
10
11
CMyString& CMystring(const CMyString &str) {
    if (*this == &str) return *this;

    delete []m_pData;
    m_pData = nullptr;

    m_pData= new char[strlen(str.m_pData) + 1]
    strcpy(m_pData, str.m_pData);

    return *this;
}

cpp基础知识

引用：引用变量是一个别名，也就是说，它是某个已存在变量的另一个名字。一旦把引用初始化为某个变量，就可以使用该引用名称或变量名称来指向变量。我们一般在类型名后添加&来表示。

引用与指针的区别：不存在空引用。引用必须连接到一块合法的内存。一旦引用被初始化为一个对象，就不能被指向到另一个对象。指针可以在任何时候指向到另一个对象。引用必须在创建时被初始化。指针可以在任何时间被初始化。

this指针：在 C++ 中，每一个对象都能通过 this 指针来访问自己的地址。this 指针是所有成员函数的隐含参数。因此，在成员函数内部，它可以用来指向调用对象。友元函数没有 this 指针，因为友元不是类的成员。只有成员函数才有 this 指针。

复制构造函数：拷贝构造函数是一种特殊的构造函数，它在创建对象时，是使用同一类中之前创建的对象来初始化新创建的对象。拷贝构造函数通常用于：通过使用另一个同类型的对象来初始化新创建的对象。复制对象把它作为参数传递给函数。复制对象，并从函数返回这个对象。

形参与实参的区别：形参出现在函数定义的地方，多个形参之间以逗号分隔，形参规定了一个函数所接受数据的类型和数量。实参出现在函数调用的地方，实参的数量与类型与形参一样，实参用于初始化形参。当形参是引用类型时，对应的实参被引用传递，引用形参是对应的实参的别名。当实参的值被拷贝给形参时，形参和实参是两个相互独立的对象，对应的实参被值传递。C++中，建议使用引用类型的形参替代指针，因为使用引用，形式上更简单，无须额外声明指针变量，也避免了拷贝指针的值。如果函数无须改变引用 形参的值，最好将其声明为const引用。

指针运算符：C++ 提供了两种指针运算符，一种是取地址运算符&，一种是间接寻址运算符*。&是一元运算符，返回操作数的内存地址。第二个运算符是间接寻址运算符*，它是&运算符的补充。*是一元运算符，返回操作数所指定地址的变量的值。

基本数据结构

数组

剑指 Offer 03. 数组中重复的数字：在一个长度为 n 的数组 nums 里的所有数字都在 0～n-1 的范围内。数组中某些数字是重复的，但不知道有几个数字重复了，也不知道每个数字重复了几次。请找出数组中任意一个重复的数字。

1
2
3
输入：
[2, 3, 1, 0, 2, 5, 3]
输出：2 或 3

这个问题有三种解法，第一种是先将数组排序，然后从前往后遍历一遍即可找到重复的数，排序的时间复杂度为O(nlogn)；第二种是利用哈希表来解决时间和空间复杂度均为O(n)，如下，还可以进一步不用新建数组，直接在原始数组上交换元素并进行比较，空间复杂度可以到O(1)；第三种是使用二分查找的思想，分别统计前1~m和m+1~n中数字出现的次数t1,mt_{1,m}和tm+1,nt_{m+1,n}，若t1,m>mt_{1,m} > m则前面的序列中存在重复数字，递归前面的子数组，后面的亦然如此，这种方法每次需要统计数字出现的次数，时间复杂度为O(n)，二分查找时间复杂度为O(logn)，总体时间复杂度为O(nlogn)，空间复杂度为O(1)。

1
2
3
4
5
6
7
8
9
10
11
12
13
// 解法二：数组作为哈希表，空间复杂度为O(n),时间复杂度为O(n)
class Solution {
public:
    int findRepeatNumber(vector<int>& nums) {
        vector<int> hash(nums.size(), 0);
        if (nums.size() == 0) return -1;
        for (int i=0; i < nums.size(); i++) {
            hash[nums[i]] ++;
            if (hash[nums[i]] > 1) return nums[i];
        }
        return -1;
    }
};
1
2
3
测试用例：
    - 长度为n的数组里包含一个或多个重复的数字
    - 无效输入测试用例（空数组，包含0——n-1之外的数字）

剑指 Offer 04. 二维数组中的查找:在一个 n * m 的二维数组中，每一行都按照从左到右递增的顺序排序，每一列都按照从上到下递增的顺序排序。请完成一个高效的函数，输入这样的一个二维数组和一个整数，判断数组中是否含有该整数。

1
2
3
4
5
6
7
8
9
10
11
12
现有矩阵 matrix 如下：
[
  [1,   4,  7, 11, 15],
  [2,   5,  8, 12, 19],
  [3,   6,  9, 16, 22],
  [10, 13, 14, 17, 24],
  [18, 21, 23, 26, 30]
]

给定 target = 5，返回 true。

给定 target = 20，返回 false。

思路：由于数组元素是递增的，那么每访问一个元素，可以排除数组中的部分元素，即从数组的右上角开始遍历，numsrow,colnums_{row, col}为当前值，当target>numsrow,coltarget > nums_{row, col}时，numsrow,colnums_{row, col}需变为numsrow,col−1nums_{row, col-1}，数组第colcol列可以排除掉；而当target<numsrow,coltarget < nums_{row, col}时，需变为numsrow+1,colnums_{row+1, col}，数组第rowrow行可以排除掉。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution {
public:
    bool findNumberIn2DArray(vector<vector<int>>& matrix, int target) {
        if (matrix.size() == 0 || matrix[0].size() == 0) return false;
        int row = 0;
        int col = matrix[0].size() - 1;
        while (row < matrix.size()  && col >= 0) {
            int nums = matrix[row][col];
            if (nums == target) return true;
            else if (nums > target) col--;  // 去掉第col列
            else row++; //去掉第row行
        }
        return false;

    }
};
1
2
3
测试用例
    - 正常输入的二维数组，正常的target
    - 特殊输入测试（输入空数组）

字符串

C中每个字符串都以字符'\0'作为结尾，所以每个字符串会有一个额外的内存开销，容易引起内存越界的情况。为节省内存，C会将常量字符串放到单独的一个内存区域，此时如果使用指针指向它的话，无论多少指针，指向的都是相同的地址。

剑指 Offer 05. 替换空格:请实现一个函数，把字符串 s 中的每个空格替换成"%20"。

输入：s = “We are happy.”
输出：“We%20are%20happy.”

思路：两种方法，第一种是暴力求解，即从头到尾遍历一遍，每发现一个空格，就在结尾添加两个元素，然后将空格后的字符串向后移动两个位置，再将'%20'插入字符串中，如下面暴力解法所示，这种方法的时间复杂度为O(n2)O(n^2)，空间复杂度为O(1)O(1)，观察可以发现后面的字符串移动了多次，这种时间消耗应该是可以避免的；第二种方法是采用双指针求解，使用p1指针倒序遍历原始字符串，使用p2指针倒序遍历新字符串，当p1指向空格是，p2顺序填入02%，这种方法的时间复杂度为O(n)O(n)，但空间复杂度也为O(n)O(n)。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
// 暴力解法
class Solution {
public:
    string replaceSpace(string s) {
        for (int i=0; i < s.size(); i++) {
            if (s[i] == ' ') {
                s += ' ';
                s += ' ';
                for (int j = s.size()-3; j >i; j--) {
                    s[j + 2] = s[j];
                }
                s[i] = '%';
                s[i+1] = '2';
                s[i+2] = '0';
            }
        }
        return s;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
// 双指针解法
class Solution {
public:
    string replaceSpace(string s) {
        int numspace = 0;
        int p1 = s.size();
        if (p1 == 0) return s;
        int p2;
        for (int i=0; i< s.size(); i++) {
            if (s[i] == ' ') numspace++;
        }
        p2 = p1 + numspace*2;
        string res(p2, ' ');
        p2 = p2 - 1;
        p1 = p1 - 1;
        while (p1 >= 0) {
            if (s[p1] != ' ') {
                res[p2] = s[p1];
                p2--;
                p1--;
            }
            else {
                res[p2] = '0';
                res[p2-1] = '2';
                res[p2-2] = '%';
                p2 = p2 -3;
                p1--;
            }
        }
        return res;
    }
};

链表

剑指 Offer 06. 从尾到头打印链表

输入：head = [1,3,2]
输出：[2,3,1]

思路：考虑两种方法，第一种需要修改链表结构，即先反转链表，然后再从头到尾进行打印这种方法的时间复杂度为O(n)O(n)， 空间复杂度为O(1)O(1)；第二种不需修改链表结构，可以递归的打印链表节点，考虑采用链表的后序遍历方法，这种方法的时间复杂度为O(n)O(n)，空间复杂度为O(n)O(n)，另外还可采用栈作为一个额外的存储结构，便于我们遍历，下面我们采用后序遍历的方法进行遍历。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
// 后序遍历求解
class Solution {
public:
    vector<int> res;
    vector<int> reversePrint(ListNode* head) {
        reverseList(head);
        return res;
    }
    void reverseList(ListNode* head) {
        if (head == nullptr) return ;
        reverseList(head -> next);
        res.push_back(head -> val);
    }

};

树

剑指 Offer 07. 重建二叉树:输入某二叉树的前序遍历和中序遍历的结果，请构建该二叉树并返回其根节点。
假设输入的前序遍历和中序遍历的结果中都不含重复的数字。

Input: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]
Output: [3,9,20,null,null,15,7]

思路：此题是一个典型的问题，根据前序遍历和中序遍历的特点，我们可以递归的处理这个问题，首先根据前序遍历找到根节点，然后在前序遍历和中序遍历中划分左右子树，直到子树为空，此方法的时间复杂度为O(n)O(n)，空间复杂度为O(n)O(n)。

具体构造思路：考虑参数上，我们需要当前的根节点，前序遍历的low与high，中序遍历的low与high，返回值需要返回构造完成之后的根节点。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
// 递归解法 -- TODO:此解法在边界上还有一点问题，后续需fix
class Solution {
public:
    TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
        return buildSubTree(preorder, 0, preorder.size() - 1, inorder, 0, inorder.size() - 1);
    }
    TreeNode* buildSubTree(vector<int> &preorder, int prelow, int prehigh, vector<int> &inorder, int inlow, int inhigh) {
        if (prelow > prehigh) return nullptr;
        if (inlow > inhigh) return nullptr;
        TreeNode* head = new TreeNode(preorder[prelow]);
       
        int inhead=INT_MAX, preright=INT_MAX;
        // 中序遍历中head节点位置
        for (int i=inlow; i <= inhigh; i++) {
            if (inorder[i] == preorder[prelow]) {
                inhead = i;
                break;
            }
        }

        // 前序遍历中左子树最后一个节点位置
        for (int i=prelow; i <= prehigh; i++) {
            if (inorder[inhead - 1] == preorder[i]) {
                preright=i+1;
                break;
            }
        }
        cout << preright << ' ' << inhead << endl;
        head -> left = buildSubTree(preorder, prelow+1, preright - 1, inorder, inlow, inhead - 1);
        head -> right = buildSubTree(preorder, preright, prehigh, inorder, inhead + 1, inhigh);
       
        
        return head;
    }
};

栈与队列

剑指 Offer 09. 用两个栈实现队列:用两个栈实现一个队列。队列的声明如下，请实现它的两个函数 appendTail 和 deleteHead ，分别完成在队列尾部插入整数和在队列头部删除整数的功能。(若队列中没有元素，deleteHead 操作返回 -1 )

输入：
[“CQueue”,“appendTail”,“deleteHead”,“deleteHead”]
[[],[3],[],[]]
输出：[null,null,3,-1]

思路：考察栈与队列的特性，在插入操作中，我们先将序列push到#1栈中，然后从#1中pop出来push到#2栈中，这样就完成了一个序列的颠倒；在删除操作中，我们简单的pop出#2栈中的数据即可。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
class CQueue {
public:
    CQueue() {

    }
    
    void appendTail(int value) {
        stack1.push(value);
    }
    
    int deleteHead() {
        if (stack2.empty()) {
            if (stack1.empty()) return -1;
            in2out();
        }
        
        int res = stack2.top();
        stack2.pop();
        return res;
        
    }
private:
    stack<int> stack1, stack2;
    void in2out() {
        while(!stack1.empty()) {
            stack2.push(stack1.top());
            stack1.pop();
        }
    }
};

算法与数据操作

查找与排序应重点掌握二分查找，归并排序，快速排序。

二维数组中搜索路径，可以尝试回溯算法，一般回溯算法用递归写会比较方便，而如果不能使用递归，则可以使用栈来模拟递归的过程。

如果问题是求最优解，且该问题可以分为多个子问题，那么我们可以尝试动态规划，自上而下的思路去处理动态规划的问题。如果动态规划中存在某个特殊的选择，那么可以采用贪婪算法。

位运算是一种特殊的算法，它是将数字表示成二进制之后对0和1进行操作，其只有与/或/异或/左移/右移5种运算。

递归与循环

剑指 Offer 10- I. 斐波那契数列：写一个函数，输入 n ，求斐波那契（Fibonacci）数列的第 n 项（即 F(N)）。斐波那契数列的定义如下：F(0) = 0, F(1) = 1
F(N) = F(N - 1) + F(N - 2), 其中 N > 1.斐波那契数列由 0 和 1 开始，之后的斐波那契数就是由之前的两数相加而得出。

答案需要取模 1e9+7（1000000007），如计算初始结果为：1000000008，请返回 1。

输入：n = 5 输出：5；
输入：n = 2 输出：1

1
2
3
4
5
6
7
8
9
10
// 纯递归解法
class Solution {
public:
    int fib(int n) {
        if (n == 0) return 0;
        if (n == 1) return 1;
        return (fib(n-1) + fib(n-2)) % (1000000007);
    }

};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
// 动态规划解法
class Solution {
public:
    int fib(int n) {
        if (n == 0) return 0;
        if (n == 1) return 1;
        int resN1 = nums[n-1] == -1 ? fib(n-1) : nums[n-1];
        int resN2 = nums[n-2] == -1 ? fib(n-2) : nums[n-2]; 
        if (nums[n] == -1) {
            nums[n] = (resN1 + resN2) % (1000000007);
        }
        return (resN1 + resN2) % (1000000007);
    }
private:
    vector<int> nums=vector<int> (1000000007);
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
// 循环+动态规划解法
class Solution {
public:
    int fib(int n) {
        if (n==0) return 0;
        if (n == 1) return 1;
        nums.push_back(0);
        nums.push_back(1);
        int res1, res2;
        for (int i=2;i <=n; i++) {
            res1 = nums[i-1];
            res2 = nums[i-2];
            nums.push_back((res1 + res2) % (1000000007));
        }
        return nums[n];
        
    }
private:
    vector<int> nums;
};

查找

剑指 Offer 11. 旋转数组的最小数字:把一个数组最开始的若干个元素搬到数组的末尾，我们称之为数组的旋转。
给你一个可能存在 重复 元素值的数组 numbers ，它原来是一个升序排列的数组，并按上述情形进行了一次旋转。请返回旋转数组的最小元素。例如，数组 [3,4,5,1,2] 为 [1,2,3,4,5] 的一次旋转，该数组的最小值为 1。  
注意，数组 [a[0], a[1], a[2], …, a[n-1]] 旋转一次 的结果为数组 [a[n-1], a[0], a[1], a[2], …, a[n-2]] 。

输入：numbers = [3,4,5,1,2]
输出：1

思路：可以直接暴力遍历一遍，即可找到要找的值，此方法的时间复杂度为O(n)O(n)；也可以采用二分查找的方法，选择最后一个元素xx作为基准，可以发现在最小值前面的元素均大于xx，在最小值后面的元素均小于xx，这样可以进行二分查找。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
public:
    int minArray(vector<int>& numbers) {
        int low = 0;
        int high = numbers.size() -1;
        
        while (low < high) {
            int p = (low + high) / 2;
            if (numbers[p] > numbers[high]) {
                low = p + 1;
            }
            else if (numbers[p] < numbers[high]){
                high = p;
            }
            else {
                high--;
            }
        }
        return numbers[low];
    }
};

回溯法

解决问题包含许多步骤，每个步骤都有多个选项，此解决方案可以看成一颗树，我们就是遍历这颗树，当某节点不满足约束条件时，则回溯到上一节点再尝试其他选项。

剑指 Offer 12. 矩阵中的路径：给定一个 m x n 二维字符网格 board 和一个字符串单词 word 。如果 word 存在于网格中，返回 true ；否则，返回 false 。

单词必须按照字母顺序，通过相邻的单元格内的字母构成，其中“相邻”单元格是那些水平相邻或垂直相邻的单元格。同一个单元格内的字母不允许被重复使用。

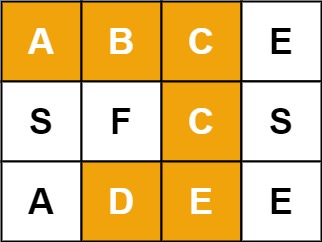
例如，在下面的 3×4 的矩阵中包含单词 “ABCCED”（单词中的字母已标出）。
image-word2

输入：board = [[“A”,“B”,“C”,“E”],[“S”,“F”,“C”,“S”],[“A”,“D”,“E”,“E”]], word = “ABCCED”
输出：true

思路：

  • 递归参数：当前矩阵的行索引i和列索引j，以及word中的索引k；

  • 终止条件：

    • 返回false：行索引越界，列索引越界，当前矩阵元素与目标字符不同，当前矩阵元素已访问过；
    • 返回true：k=word.size()−1k=word.size() -1；

  • 递推工作：

    1. 标记当前矩阵元素：board[i][j]=′′board[i][j]=''，表示此元素已访问过，防止以后搜索时重复访问；
    2. 搜索下一单元格，有四个方位。使用||进行连接

  • 返回值：返回bool值，代表是否搜索到目标字符串。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution {
public:
    bool exist(vector<vector<char>>& board, string word) {
        if (board.size() == 0 || word.size() == 0) return false;
        row = board.size();
        col = board[0].size();
        for (int i=0; i < row; i++) {
            for (int j=0; j < col; j++) {
                if (backtracking(board, word, i, j, 0)) return true;
            }
        }
        return false;
    }
private:
    int row, col;
    bool backtracking(vector<vector<char>>& board, string word,int i, int j, int k) {
        if (i >= row || i < 0 || j >= col || j < 0 || board[i][j]!=word[k]) return false;
        if (k == word.size() -1) return true;
        board[i][j] = '\0';
        bool res = backtracking(board, word, i-1, j, k+1) || backtracking(board, word, i+1, j ,k+1) || backtracking(board, word, i, j-1, k+1) || backtracking(board, word, i, j+1, k+1);
        board[i][j] = word[k];
        return res;
    }
};

地上有一个m行n列的方格，从坐标 [0,0] 到坐标 [m-1,n-1] 。一个机器人从坐标 [0, 0] 的格子开始移动，它每次可以向左、右、上、下移动一格（不能移动到方格外），也不能进入行坐标和列坐标的数位之和大于k的格子。例如，当k为18时，机器人能够进入方格 [35, 37] ，因为3+5+3+7=18。但它不能进入方格 [35, 38]，因为3+5+3+8=19。请问该机器人能够到达多少个格子？

输入：m = 2, n = 3, k = 1
输出：3

思路：此题与上题一样，均使用回溯算法进行求解

  • 递归参数：矩阵的行索引i与列索引j，以及约束条件k;
  • 终止条件：
    1. 返回0：行索引与列索引越界，行索引与列索引突破约束条件；
    2. 返回具体可移动格子数res：
  • 递推工作：
    1. 标记当前元素：如果当前元素已经被访问过了，就将矩阵值设为1；
    2. 搜索下一步骤：从4个方向寻找，用||进行连接；
  • 返回值：返回res为从该节点出发可到达的格子数；
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
class Solution {
public:
    int movingCount(int m, int n, int k) {
        vector<vector<int>> board(m, vector<int>(n, 0));
        row = m; col = n;
        return backtracking(board, 0, 0, k);
    }
private:
    int row, col;
    int backtracking(vector<vector<int>>& board, int i, int j, int k) {
        if (i < 0 || i >= row || j < 0 || j >= col || !digCompare(i, j, k) || board[i][j] == 1) return 0;
        board[i][j] = 1;
        int res = backtracking(board, i-1, j, k) + backtracking(board, i+1, j, k) + backtracking(board, i, j-1, k) + backtracking(board, i, j+1, k) + 1;
        return res;
    }
    bool digCompare(int i, int j, int k) {
        int num1=0, num2=0;
        while (i !=0) {
            num1 += i % 10;
            i = i / 10;
        }
        while ( j !=0) {
            num2+= j % 10;
            j = j / 10;
        }
        if (num1 + num2 > k) return false;
        else return true;
    }
};

动态规划与贪心算法

问题要能分解成若干子问题以及重叠子问题结构，则可采用动态规划进行求解。

给你一根长度为 n 的绳子，请把绳子剪成整数长度的 m 段（m、n都是整数，n>1并且m>1），每段绳子的长度记为 k[0],k[1]…k[m-1] 。请问 k[0]k[1]…*k[m-1] 可能的最大乘积是多少？例如，当绳子的长度是8时，我们把它剪成长度分别为2、3、3的三段，此时得到的最大乘积是18。

输入: 2
输出: 1
解释: 2 = 1 + 1, 1 × 1 = 1

思路：分析动态规划问题的思路，从上往下分别问题（需分析是否能分解成若干子问题， 子问题有无重叠），从下往上求解（使用一个一维或二维数组存放结果）。

  • 确定dp数组下标意义：dp[i]dp[i]表示长度为i的绳子的所有连乘积结果的最大值；
  • 初始化状态：
    1. 当i=0i=0时，f(i)=0f(i)=0；当i=1i=1时，f(i)=1f(i)=1；当i=2i=2时，f(i)=1f(i)=1;
  • 确定状态转移方程：长度为i的绳子在切出长度为j时有三种可能的方案
    1. 直接相乘，即j⋅(i−j)j\cdot (i-j);
    2. 其中一个继续可分，即j⋅dp[i−j]j \cdot dp[i-j]和dp[j]⋅(i−j)dp[j] \cdot (i-j)；
    3. 两者皆可分，即dp[j]⋅dp[i−j]dp[j] \cdot dp[i-j];
  • 遍历顺序：从底向上遍历；
    1. i的取值范围：3~n;
    2. j的取值范围：2~i-1;
  • 返回值：dp[n];
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
// 动态规划求解
class Solution {
public:
    int cuttingRope(int n) {
        if (n < 0) return 0;
        if (n == 2) return 1;
        if (n ==1) return 1;
        vector<int> res(n+1, 0);
        res[0] = 0;
        res[1] = 1;
        res[2] = 1;
        res[3] = 2;
        
        for (int i=3; i<= n; i++) {
            int max_num = 0;
            for (int j=2; j < i; j++) {
                int num = max({j * (i-j), j * res[i-j], res[j] * (i-j), res[j] * res[i-j]});
                max_num = max_num > num ? max_num: num;
            }
            res[i] = max_num;
        }
        return res[n];
    }
};

位运算

位运算主要有与，或，异或以及左移，右移这五种运算。其中右移有一点特殊，对于有符号数，右移后左边的值需补其符号位，若为正数，则全补0，负数则全补1；

剑指 Offer 15. 二进制中1的个数:编写一个函数，输入是一个无符号整数（以二进制串的形式），返回其二进制表达式中数字位数为 ‘1’ 的个数（也被称为 汉明重量).）。

输入：n = 11 (控制台输入 00000000000000000000000000001011)
输出：3
解释：输入的二进制串 00000000000000000000000000001011 中，共有三位为 ‘1’。

思路：每一位与0做异或，结果为1则为1，结果为0则为0；也可以与1做与运算，结果为0则为0，结果为1则为1；

1
2
3
4
5
6
7
8
9
10
11
12
13
// 与运算
class Solution {
public:
    int hammingWeight(uint32_t n) {
        int count = 0;
        uint32_t flag=1;
        while(flag) {
            if (n & flag) count++;
            flag = flag << 1;
        }
        return count;
    }
};
cpp
#刷题
【剑指offer-2】基础知识
http://example.com/2022/05/28/【剑指offer-2】基础知识/
作者
leegaojun
发布于
2022年5月28日
许可协议